The hidden mathematics of your garden.

One of the most enchanting moments I experienced in my grandmother's garden was the revelation of the hidden presence of the Fibonacci sequence in the intricate patterns of flowers, leaves, pine cones, and trees. This discovery unfolded during my high school years at Colégio Estadual do Paraná when my mathematics teacher selected four of us to represent our school at the FEMUCI Municipal Science Fair and the II Exponaci - National Science Exhibition in Curitiba, Brazil.

Among the various themes proposed for exploration, one particularly captured our imagination: uncovering and demonstrating the Fibonacci sequence woven throughout a garden's tapestry. It was a transformative realization that mathematics wasn't confined to textbooks but thrived in the living world around us.

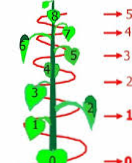
Take a moment to observe your garden closely. You'll notice that the leaves of plants rarely align perfectly vertically. Instead, they tend to spiral around the stem. Consider a leaf at the stem's base as the starting point, labeled as zero. Count the number of leaves until you return to the zero leaf, and you'll often find this count falls within the Fibonacci sequence. Similarly, counting the number of turns before leaf overlap reveals Fibonacci numbers again and again. Why does nature exhibit this pattern repeatedly, even in the growth of plants?

The answer lies in efficiency. Nature optimizes space utilization, much like packing objects to minimize waste. If asked how to best pack objects, you'd consider their shapes. Square objects fit snugly in square structures, while round ones nestle better in hexagons. But what about arranging leaves or seeds as they continue to grow?

Remarkably, nature employs the same pattern for organizing seeds, petals, and leaves. This pattern, determined by an angle of rotation from a central point, ensures effective arrangements as the plant expands. Botanists have observed this pattern emerging from meristems—small groups of cells at the growth tips of branches, buds, and petals. These cells spiral outwards, each maintaining a consistent angle relative to the center.

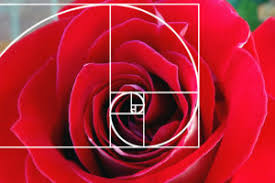
The remarkable aspect is that a single angle suffices, regardless of the plant's size. Leaves receive optimal sunlight without excessive overlap, thanks to this angle, which corresponds to a fractional value of the golden ratio: 0.618034.

The spirals visible in flowers and fruits often align with Fibonacci numbers. Sunflowers boast 55 and 89 spirals, daisies exhibit 21 and 34, and pineapples typically feature 8 and 13 or 5 and 8 spirals. These arrangements aren't encoded in genetic blueprints but are the outcomes of practical evolution. By efficiently packing seeds, plants maximize resource use, earning evolutionary advantages over less efficient counterparts.

With fervor and excitement, we set up our exhibit, adorned with an array of vibrant plants, eager to share our newfound fascination with the public attending the event. Using long strips of cardboard, we meticulously crafted circles around the stems of plants, showcasing the elegant spiral arrangement of leaves—a hallmark of the Fibonacci sequence.

Participating in the exhibition was an honor, and we poured our hearts into the presentation. The culmination of our efforts was met with the ultimate reward: first prize. It was a testament not only to our dedication but also to the universal appeal and relevance of mathematics, bridging the gap between theory and the natural world in a way that captivated both our minds and those of our audience.

Fibonacci numbers' prevalence in nature stems from their association with the golden ratio, admired by the Greeks for its natural and pleasing proportions. Thus, the Fibonacci sequence emerges as a testament to nature's elegant efficiency and the beauty of mathematical principles embedded in the fabric of life.

Are you motivated to discover the beauty of mathematic in your garden?

Info about Fibonacci:

Leonardo Pisano Fibonacci (1170–1240 or 1250) was an Italian number theorist. Fibonacci played a pivotal role in introducing the Hindu–Arabic numeral system to the Western world, notably through his influential work "Liber Abaci" (Book of Calculation) published in 1202. Within this text, he not only elucidated the principles of this numeral system but also introduced Europe to the sequence of numbers that now bear his name, known as the Fibonacci sequence.

The Fibonacci sequence is the series of numbers where each number is the sum of the two preceding numbers. For example,

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Mathematically we can describe this as:

xn= xn-1 + xn-2

My memories :

1. Draft showing the leaves distribution and the Fibonacci sequence.

2. Feira Municipal de Ciências, Exposição Nacional de Cięncias, Curitiba, Brazil. Certification: "As matemáticas e suas com...sequências".

3. Colégio Estadual do Paraná, Curitiba, Brazil.